ÚLOHY – MOFO 2012

MATEMATIKA


1.      M Najděte všechna přirozená čísla n, pro něž číslo  je také přirozené.

1.      S Řešte rovnici .

2.      M Ukažte, že číslo  je vždy druhou mocninou přirozeného čísla.

2.      S O obsahu S trojúhelníku platí: , kde a, b, c jsou velikosti stran. Určete velikost úhlu a.

3.      M Pět děvčat starších deseti let bylo dotazováno na své stáří. K tomu odpovědělo pravdivě každé z nich:

a)      Dáda není ani nejmladší ani nejstarší;

b)      Bára je mladší než Cilka, ale starší než Dáda;

c)      Cilka je stará 14 let;

d)      Bára i Cilka jsou obě mladší než Elsa;

e)      Elsa je o 5 let starší než Asta.

3.      S Najděte všechny dvojice x, y nezáporných celých čísel, které splňují rovnici .

4.      M Nahraďte v partituře písmena číslicemi tak, aby platilo: 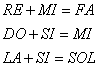. DOREMIFASOL = ?

4.      S Je dána posloupnost , tj. posloupnost, jejíž n-tý člen je pro všechna přirozená čísla n roven celé části čísla . Určete součet .

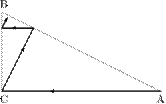
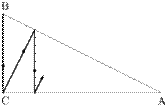
5.      Z vrcholu A do vrcholu B pravoúhlého trojúhelníku vede lomená čára, jejíž úseky jsou kolmé střídavě k odvěsně BC a k přeponě AB. Celková délka lomené čáry je 260. Z vrcholu B do vrcholu A téhož trojúhelníku vede lomené čára, jejíž úseky jsou kolmé střídavě k odvěsně AC a k přeponě AB. Celková délka této lomené čáry je 78. Jaké jsou délky stran trojúhelníku ABC? 

 

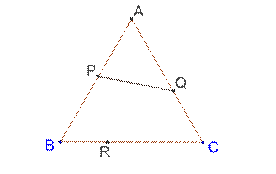
6.      Rovnostranný trojúhelník ABC o straně délky 3 přeložíme podle úsečky PQ tak, že bod A splyne s bodem R  úsečky BC a platí  Jaká je délka úsečky PQ?

7.      Výška rovnostranného trojúhelníku ABC je rovna 1. V jaké vzdálenosti od bodu A je nutno narýsovat přímku rovnoběžnou se základnou AB tak, aby dělila trojúhelník  ABC na dvě části se stejným obsahem?

 

8.      Kolik uspořádaných dvojic  přirozených čísel splňuje rovnici

?

 

9.      Dvě kruhové desky o průměrech 6 cm a 18 cm jsou umístěny v rovině tak, že mají vnější dotyk a jsou obepnuty provázkem. Jaká je délka tohoto provázku?

 

10.  Dvě různá trojciferná čísla jsou obě dělitelná 21. Druhé z nich vznikne z prvního čísla tak, že zaměníme první cifru se třetí. Která jsou to čísla?

 

 

FYZIKA


1.      Cyklista koná rovnoměrný přímočarý pohyb. Ve vzdálenosti 2 000 m od místa startu se obrátí a po téže trajektorii projede v opačném směru 2 400 m a zastaví. Jaká je velikost posunutí a její směr? Jaká je dráha jeho pohybu?

2.      Cyklista vyjíždí kopec stálou rychlostí, přičemž působí na pedál jízdního kola průměrnou silou o velikosti 150 N. Délka kliky pedálu je 25 cm, doba jedné otáčky pedálu je 2 s. Určete průměrný výkon cyklisty.

3.      Z kopce vysokého 2 m a se základnou 5 m sjíždí sáňky. Na rovině až do zastavení urazí dráhu 35 m. Určete koeficient smykového tření saní pro tento pohyb.

4.      Ohebný provázek délky L leží na hladkém vodorovném stole a je orientován kolmo k okraji stolu. Jeden jeho konec se nachází při okraji stolu. Po krátkém potažení sjíždí ze stolu. Jak závisí zrychlení a rychlost provázku na délce jeho části x, kterou visí ze stolu? Jakou bude mít rychlost v okamžiku, kdy opustí stůl?

5.      Deska, která je rozdělena na pět stejných částí, začíná sjíždět z nakloněné roviny. U přední hrany desky se na nakloněné rovině nachází značka, kolem níž projel první úsek za 2 s. Za jakou dobu projede kolem této značky poslední úsek? Pohyb desky je rovnoměrně zrychlený.

6.      Vytvoříme-li ve vodiči o obsahu příčného řezu 10 mm2 elektrické pole o intenzitě 0,4 V/m, pohybují se volné elektrony ve vodiči tak, že proud bude mít hodnotu 23,5 A. Jaký je měrný odpor vodiče? Pomocí tabulek se pokuste odhadnout, z jakého kovu by vodič mohl být vyroben.

7.      Mezi každým párem z n bodů je vložen kondenzátor kapacity C.  Určete kapacitu soustavy kondenzátorů mezi libovolnými dvěma body.

8.      Na vodorovné podložce se nachází válcová nádoba příčkou rozdělená na dvě stejné části.    V jedné polovině je kyslík, ve druhé dusík. Tlak plynu v části s dusíkem je dvojnásobný vzhledem k tlaku v části vyplněné kyslíkem. O jakou vzdálenost se posune po podložce nádoba, jestliže se příčka stane propustnou? Délka nádoby je 20 cm, hmotnost nádoby         a smykové tření zanedbejte. Děj považujte za izotermický.

9.      Spočtěte četnost vzniku neutrin ve Slunci. Předpokládejte, že veškerá produkce energie je dána proton-protonovým řetězcem. Spočtěte četnost dopadu neutrin na Zemi. Výkon Slunce je 3,9·1026 W, atomová hmotnostní jednotka u = 1,661·10-27 kg, střední vzdálenost Země       a Slunce 149,59787·109 m, poloměr Země 6378 km. Relativní atomové hmotnosti si stáhněte z webu http://physics.nist.gov/cgi-bin/Compositions/stand_alone.pl nebo použijte periodickou soustavu prvků.

10.  Na každém konci provazu vedeném přes kladku je v téže výšce opice. V určitém okamžiku a) začne jedna z opic šplhat vzhůru rychlostí v vzhledem k provazu. Jakou rychlostí se tato opice blíží ke kladce? Co se děje s druhou opicí? b) začnou obě opice šplhat vzhůru, jedna rychlostí v a druhá rychlostí dvojnásobnou vzhledem k provazu. Jakou rychlostí se opice blíží ke kladce? V obou případech mají opice stejnou hmotnost.