ÚLOHY -


MATEMATIKA
  1. Dokažte, že pro každé přirozené číslo n je číslo n(n + 1)(n + 2)(n + 3) + 1 druhou mocninou přirozeného čísla.
  2. V pásu mezi dvěma rovnoběžkami je umístěn bod A. Ze všech pravoúhlých trojúhelníků s pravým úhlem u vrcholu A a dalšími vrcholy vždy na daných rovnoběžkách najděte ten, který má nejmenší obsah.
  3. Dokažte, že pokud jsou p, p2 + 2 prvočísla, pak je prvočíslo také p3 + 2.
  4. Z města H do města K povede trať nové dálkové autobusové linky. Komise odborníků rozhoduje, ve kterých z měst A, B, C, D, která leží na této trati, má být zřízena zastávka. Byly podány tyto návrhy: 1. člen komise: Není vhodné zřizovat zastávku v obou z měst B a C, ale je nutné, aby autobus stavěl v B nebo v D.
    2. člen komise: Autobusová zastávka by měla být určitě v C nebo v B; jsem dále proti tomu, aby byla současně v městech A a C.
    3. člen komise: Není možné, aby byla zastávka zřízena v B a přitom nebyla zřízena v A. Jsem také proti tomu, aby autobus stavěl ve všech třech městech B, C a D.
    Ve kterých z měst A, B, C, D byly zbudovány zastávky této autobusové linky, víme-li, že všechny návrhy byly respektovány a žádný další návrh nebyl podán? Má-li úloha více řešení, uveďte všechny.
  5. Najděte všechna přirozená čísla n, pro která je podíl (19n + 17)/(7n + 11) celé číslo.
  6. Uvažme trojúhelník ABC a následující tvrzení:
    1. úhel při vrcholu B je pravý
    2. úhel při vrcholu A má velikost 30o
    3. |AB| = 2|BC|
    4. |AC| = 2|BC|.
    Víme, že platí právě dvě z těchto tvrzení a že |BC| = 1. Jaký je obvod trojúhelníku ABC? Určete všechna řešení.
  7. Nad úsečkou AB = 2a (a > 0) jako nad průměrem sestrojme polokružnici k o středu S. Označme úsečku SC ⊥ AB, která je poloměrem polokružnice k. Nad úsečkou SC jako nad průměrem sestrojme kružnici l se středem O = SSC. Sestrojte kružnici m, která se dotýká polokružnice k, kružnice l a úsečky AB. Určete její poloměr v závislosti na daném čísle a.
  8. Rovnostrannému trojúhelníku XYZ je vepsána kružnice. Označme A, B průsečíky této kružnice s daným trojúhelníkem. Body A, B rozdělí kružnici na dva oblouky. Nechť kratší oblouk má velikost 1. Jaký je obsah kruhové úseče vymezené tímto kratším obloukem?
  9. Dvě čísla sečteme, odečteme, vynásobíme a vydělíme. Sečteme-li všechny výsledky, dostaneme číslo 243. Najděte všechny dvojice výchozích čísel.
  10. Nechť 123456789101112131415 … je posloupnost přirozených čísel. Která cifra je na 2011. místě?
    11. 8. 9. 10.



FYZIKA
  1. Sportovec vrhá kladivo do vzdálenosti l0 = 70 m po trajektorii umožňující maximální dolet. Jak velká síla působí na jeho ruce v okamžiku těsně před tím, než upustí lanko? Hmotnost kladiva je m = 5 kg. Předpokládejte, že během urychlování se kladivo pohybuje ve vertikální rovině po trajektorii tvaru kružnice. Zanedbejte odpor vzduchu a hmotnost lanka.
    1. Jaký musí být maximální koeficient statického tření mezi pneumatikami automobilu a asfaltem, aby se automobil mohl pohybovat rychlostí v = 100 km/h v zatáčce poloměru R = 200 m, aniž by dostal smyk?
    2. Automobil s pohonem čtyř kol se rozjíždí z klidu po vozovce, která tvoří oblouk poloměru R = 100 m. Pohyb automobilu začíná v místě, jehož poloha je popsána úhlem a = 30°. Jakou maximální rychlostí může automobil vyjet na horizontální úsek vozovky, je-li koeficient statického tření kol o povrch vozovky f = 0,3?
  3. Po vnitřní straně pláště kužele, který se pohybuje vzhůru se zrychlením a, opisuje kulička kružnici poloměru R. Určete periodu T rotačního pohybu kuličky. Úhel při vrcholu kužele má velikost 2a.
  4. Na koncích tyče délky l a zanedbatelné hmotnosti jsou umístěny malé kuličky o hmotnostech m1 a m2 (m1 > m2). Středem tyče kolmo na tyč prochází pevná osa, kolem které může bez odporu rotovat. Tyč je uvedena do vodorovné polohy a poté spuštěna. Vyjádřete úhlovou rychlost a sílu, kterou tyč s kuličkami prochází rovnovážnou polohou.
  5. Vypočtěte vazebnou energii jader deuteria 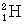, tritia 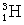a helia 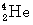(v MeV).
    Částice m[u] E[MeV] Neutrální atom m[u]
    e 0,00055 0,511 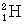2,0141
    p 1,00728 938,3 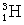3,01605
    n 1,00866 939,6 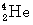4,00260
  6. Vlak se pohyboval první polovinu dráhy rychlostí 1,5-krát větší než druhou polovinu dráhy. Průměrná rychlost vlaku na celé dráze dosáhla 43,2 km/h. Jaké jsou průměrné rychlosti v první a druhé polovině dráhy?
  7. Na obrázku jsou grafy závislosti rychlosti na čase dvou hmotných bodů, které se pohybují po jedné přímce z totožného výchozího místa. Jsou známy časy t1 a t2. Ve kterém okamžiku t3 se setkají? Nakreslete graf závislosti polohy obou hmotných bodů, dané souřadnicí x, na čase.
  8. Litinová dutá koule plove na vodě tak, že je její polovina nad hladinou. Vypočtěte objem dutiny, je-li hmotnost koule 5000 g a hustota litiny 7,8 g/cm3.
  9. Jaká energie se uvolní při termojaderné reakci

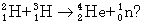
    Hodnoty potřebné k výpočtu převezměte ze zadání páté soutěžní úlohy.
  10. O kolik procent je nutno zmenšit délku matematického kyvadla, aby kmitalo se stejnou periodou ve výšce 10 km jako při povrchu Země?