Úlohy MOFO 2005 - MATEMATIKA

 

1.      Dokažte, že pro platí:

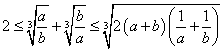
2.      Pro kladná dokažte:

 

Kdy platí rovnost?

 

3.      Máme šachovnici o rozměrech 2n × 2n políček, na které chybí jedno (libovolné) políčko.

K dispozici máme neomezený počet dílků, z nich každý sestává ze tří políček šachovnice ve tvaru L (viz obrázek).

Ukažte, že šachovnici je možno pokrýt dílky tak, aby se žádné dílky nepřekrývaly a přitom byla celá šachovnice (až na chybějící políčko) pokrytá.



4.      Číslo 3025 je zajímavé tím, že je můžeme rozdělit na dvě části, které pak sečteme, umocníme a dostaneme zase číslo 3025:

(30 + 25)2 = 3025

Najděte další taková čísla.

5.      Kvádr, jehož výška se rovná úhlopříčce podstavy je tvořen přesně krychličkami o hraně 1cm. Obsah základny se rovná násobku 311850 a neznámého přirozeného čísla. Vypočtěte výšku kvádru (nejmenší možnou).

6.      Najděte všechna přirozená čísla n, které jsou menší než 100 a mají tu vlastnost, že druhé mocniny čísel 7n+5 a 4n+3 končí stejným dvojčíslím.

7.      Zjistěte, zda je číslo 191998 + 981999 dělitelné devíti.

 

8.      Najděte všechny trojúhelníky ABC, pro které platí a + va = b + vb.

 

9.      Zjistěte, jak pokračuje tato posloupnost: J, D, T, Č, P, Š, ... .

 

10.  TRIÁDY

 

Úlohy MOFO 2005 - FYZIKA

 

Zadání soutěžních příkladů je vytištěno tučně!

 

1. Motorová loďka překoná vzdálenost mezi dvěma body A a B pluje-li ve směru proudu řeky za dobu 3 s a proud řeky za dobu 12 s. Jak dlouhou dobu potřebuje loďka na zpáteční cestu?

2. Chodec se po rovnoměrně jedoucím eskalátoru dopraví dolů za 1 min za předpokladu, že jde stálou rychlostí ve směru pohybu eskalátoru. Půjde-li stejným směrem 2-krát rychleji, bude dole za 45 s. Za jak dlouho bude dolů dopraven, bude-li na eskalátoru stát?

3. Člověk běží po eskalátoru. Poprvé napočítal 50 schodů, běžel-li stejným směrem trojnásobnou rychlostí, napočítal jich 75. Kolik by jich napočítal na stojícím eskalátoru?

4. První vagon vlaku projel kolem pozorovatele za dobu 1 s, druhý 1,5 s. Délka každého vagonu je 12 m. Určete zrychlení vlaku a jeho rychlost v okamžiku, kdy začal projíždět vlak kolem pozorovatele. Nechť je pohyb vlaku rovnoměrně zrychlený, přímočarý.

5. Těleso je vrženo svisle vzhůru s počáteční rychlostí v0. V okamžiku, kdy dosáhlo vrcholu výstupu, bylo vrženo ze stejného místa a se stejnou počáteční rychlostí těleso druhé. V jaké výšce se tělesa střetnou?

6. Cíl, nacházející se na kopci, vidíme z místa ostřelování pod úhlem a. Horizontální vzdálenost děla od cíle je L. Střela letí z děla pod úhlem b >a. Určete počáteční rychlost střely, která zasáhne cíl. Zanedbejte odpor vzduchu. Pro jaký úhel b0 bude dostřel podél nakloněné roviny, která svírá s rovinou vodorovnou úhel a, maximální?

7. Těleso dopadne na nakloněnou rovinu z výšky h a pružně se odrazí. Za jak dlouho opět dopadne na nakloněnou rovinu? Jak vypočtená doba závisí na sklonu nakloněné roviny?

8. Elektron o rychlosti 5.107 m/s a proton o rychlosti 108 m/s se pohybují přímočaře proti sobě. Jaká je jejich vzájemná rychlost?

9. Elektrický obvod se skládá ze tří vodičů stejné délky, které jsou zhotoveny ze stejného materiálu (Obrázek 1.). Průřezy vodičů jsou 1 mm2, 2 mm2, 3 mm2. Rozdíl potenciálů na koncích obvodu je 12 V. Určete úbytek potenciálů na každém vodiči.

10. Kámen hmotnosti 50 g vržený pod určitým úhlem k horizontální rovině z výšky 20 m nad povrchem země rychlostí 18 m/s dopadl na zem rychlostí 24 m/s. Určete práci, které v průběhu pohybu vykonaly síly odporu vzduchu.

11. Závažím hmotnosti 500 kg, které je spouštěno z výšky 1,2 m, je vtloukána do země pilota. Díky jednoho úderu se posune do podloží o 2 cm. Určete střední sílu, kterou na pilotu závaží během úderu působí a dobu trvání pronikání piloty do podloží v průběhu jednoho úderu. Hmotnost piloty je mnohem menší ve srovnání s hmotností závaží.

12. Ocelová koule hmotnosti 20 g, která padá z výšky 1 m na ocelovou desku se odrazí od desky do výšky 81 cm. Najděte: a) impuls síly, který během úderu na desku působí, b) uvolněné teplo v průběhu úderu.

13. Lehká koule začíná volně padat, po uražení dráhy l pružně se srazí s těžkou deskou, která se pohybuje vzhůru rychlostí u. Do jaké výšky, měřené vzhledem k vztažné soustavě spojené se zemí, se dostane koule po nárazu?

14. Dvě závaží o hmotnostech 10 kg a 15 kg visí na nitích délky 2 m tak, že se vzájemně dotýkají. Menší závaží bylo odkloněno o 60° a spuštěno. Jak vysoko obě závaží vystoupají, byl-li náraz dokonale nepružný? Jaké se přitom uvolní teplo?

15. Koule hmotnosti m, která se pohybuje rychlostí v, se srazí s koulí o hmotnosti m/2 stojící na vodorovné podložce. Po rázu první koule vychýlí svůj směr pohybu o 30°. Určete rychlosti koulí po rázu.

16. Navrhněte metodu, jak změřit průměr vzduchové bubliny ve skleněné kouli.

17. Stěny válcové nádoby, píst plochy 1 dm2 a přepážka nechť jsou zhotoveny z dokonale izolujícího materiálu. Přepážka se otevře v případě, že je tlak v pravé komoře větší než v levé. V počátečním stavu v levé části válce délky 11,2 dm se nachází 12 g helia, v pravé části stejných rozměrů 2 g helia, v obou komorách je stejná teplota 0°C. Vnější tlak činí 105 Pa. Měrná tepelná kapacita helia při stálém objemu je 3,15.103 J.K-1.kg-1, při stálém tlaku 5,25.103 J.K-1.kg-1. Pomalu posouvejme píst směrem k přepážce s chvilkovou zastávkou v okamžiku otevření přepážky. Poté dokončeme přesun pístu až k přepážce. Jakou práci přitom vykonáme?

18. Závaží o hmotnosti 50 kg je zavěšeno uprostřed drátu ABC (viz. Obrázek).

AC = CB = 5 m, AB = m. Určete napěťové síly drátu.

19. Dvě nakloněné dokonale hladké roviny, které svírají s vodorovnou rovinou úhly x a j tvoří nehybný klín. Na těchto rovinách leží hranoly stejné hmotnosti spojené vláknem přes kladku. Jakou rychlost budou mít hranoly, projdou-li od začátku pohybu vzdálenost d?

20. Kovový proužek dlouhý 6,5 cm, široký 0,85 cm a tlustý 0,76 mm se pohybuje konstantní rychlostí v ve směru nejdelší hrany proužku v magnetickém poli o indukci B, která je kolmá k ploše proužku a má velikost 1,2 mT. Hallovo napětí napříč proužkem je 3,9 mV. Vypočtěte velikost rychlosti v.

21. a) Vnější, resp. vnitřní poloměry dutého válcového vodiče jsou 2 cm, resp. 1,8 cm. Vodičem protéká proud I = 100 A rovnoměrně rozložený v celém průřezu vodiče. b) Na obrázku je řez dlouhým přímým koaxiálním kabelem. Každým z vodičů protéká co do velikosti stejný, ale co do orientace opačný proud I = 120 A rovnoměrně rozložený po celém průřezu vodiče. a = 2 cm, b = 1,8 cm, c = 0,4 cm. Diskutujte závislost magnetické indukce na vzdálenosti od osy vodiče.